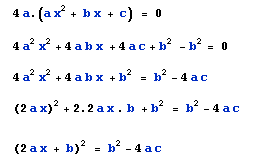Number of copies

Something very interesting happened yesterday. One of my friends was going to give a presentation in front of a group of people (24 in total), he prepared a work with other three guys (a group of 4 people).
They thought that it would be nice if everyone in the audience has a copy of the presentation slides (so they can take notes, for example). The presentation had 30 slides, my friend went to the copy center and asked for 24 copies. The guy who was there told him that he had a lot of people in the queue and he couldn't do all the copies for him, he could do only 10 as much (it was late, the most probable thing is that he was tired and didn't want to work). My friend left the copy center without any copy (really upset), told what had happened to his classmates. As they needed the copies, they decided to go to the copy center and ask for 6 copies each (so they will have the 24 copies and they avoid any problem with the problematic guy). They resolved their problem and gave the presentation, but they left me a doubt in my head. In how many ways they could distributed the number of copies so they can have 24 copies in total?, forget about the money....

So, bassically the problem is,

\begin{equation}
x_1 + x_2 + x_3 + x_4 = 24\;\;\;where\;\;\;x_i\leq 10\;\;for\;\;0\leq i \leq 4
\end{equation}

I now have an equation, I feel relaxed...


Consider only the equation, forget about the $x_i\leq 10$ restriction, counting the number of solutions of that equation is like thinking that we have 24 balls and we want to distribute the 24 balls between 4 children.

So, the solution of the equation is a known problem, it is a selection, with repetition, of size 24 from a collection of size 4. What?!?!, yes, this is one of the mathematical things that are simpler to see the formula than the description.

we can say then that the number of solutions of the equation is $|S|=\displaystyle\binom{4+24-1}{24}$.

So we have the solution of the equation, which was not what I wanted, but we are quite close. If I do $|S|$ (number of solutions) minus all the solutions in $S$ that does not satisfy the condition $x_i\leq10$ I will have the number of ways the guys could had distributed their copies. (see the inclusion and Exclusion Principle)


I need to find the solution of the equation,

\begin{equation}
x_1 + x_2 + x_3 + x_4 = 24\;\;\;where\;\;\;x_i\geq 11\;\;for\;\;0\leq i \leq 4
\end{equation}

we say that solution $x_1,x_2,x_3,x_4$ satisfies condition ci, where $1\leq i\leq 4$, if $x_i\geq 11$. So the answer of our initial problem is $N(\overline{c_1}\;\overline{c_2}\;\overline{c_3}\;\overline{c_4})$ (find solutions don't satisfy $c_1$ and $c_2$ and $c_3$ and $c_4$).

$N(\overline{c_1})$ is equal to find,

\begin{equation}
(x_1 + 11) + x_2 + x_3 + x_4 = 24\;\;\;where\;\;\;x_i\geq 0\;\;for\;\;0\leq i \leq 4
\end{equation}

which is equal to:

\begin{equation}
x1 + x2 + x3 + x4 = 13\;\;\;where\;\;\;x_i\geq 0\;\;for\;\;0\leq i \leq 4
\end{equation}

That is the same as what we solved before!!

So, $N(c_1) =\displaystyle\binom{4+13-1}{13}$, as it is a simmetric problem we have $N(c_1) = N(c_2) = N(c_3) = N(c_4)$, so $|S_1| = \displaystyle\binom{4}{1} \displaystyle\binom{4+13-1}{13}$ (the total number of solutions individually)

We need also to calculate $N(c_i,c_k)$ where $0\leq i,k\leq 4$ and $i \neq k$, which is also easy,

\begin{equation}
(x_1 + 11) + (x_2+11) + x_3 + x_4 = 24\;\;\;where\;\;\;x_i\geq 0\;\;for\;\;0\leq i \leq 4
\end{equation}


\begin{equation}
x1 + x2 + x3 + x4 = 2\;\;\;where\;\;\;x_i\geq 0\;\;for\;\;0\leq i \leq 4
\end{equation}


So $N(c_1,c_2) = \displaystyle\binom{4+2-1}{2}$, as it is a simmetric problem $|S_2| = \displaystyle\binom{4}{2} \displaystyle\binom{4+2-1}{2}$ ( the total number of solutions of (2) where $0\leq i,k\leq 4$ and $i \neq k$)

$N(c_i,c_j,c_k) = 0$ and $N(c_i,c_j,c_k,c_t) = 0$ (do the same thing as we did before and you get a negative number on the right side of the equation)

So now we have all the calculations we need

$N(\overline{c_1}\;\overline{c_2}\;\overline{c_3}\;\overline{c_4}) = |S| - |S1| + |S2| - |S3| + |S4| $

$N(\overline{c_1}\;\overline{c_2}\;\overline{c_3}\;\overline{c_4}) = \displaystyle\binom{4+24-1}{24} - \displaystyle\binom{4}{1} \displaystyle\binom{4+13-1}{13} + \displaystyle\binom{4}{2} \displaystyle\binom{4+2-1}{2} - 0 + 0 $

$N(\overline{c_1}\;\overline{c_2}\;\overline{c_3}\;\overline{c_4}) = \frac{27!}{24! 3!} - \frac{4!}{1! 3!} \frac{16!}{13! 3!} + \frac{4!}{2! 2!} \frac{5!}{2! 3! }= 745 $

Again, who can ever thing that maths are awful!

Looking through my dog's eyes (first approach)

Hello, it's been a long time, but I didn't have something interesting to tell, I've been reading about ontological Engineering which is not something very exciting for everyone. 

I did this last month, and never improved it, so I decided that I could show you something without being completed. I was kind of boring and was thinking about how my dogs can see (as you can see, I live like a  rock star). I mean, do they seen in black and white?, do they see colors? how is their perspective of the world?, well, I participate on a forum about dogs (I have a bullmastiff) and one guy talked about this topic once. He posted these images.

The first one is the human vision, and the second one is the dog vision. If we consider that this is true.... Let's start doing a first analysis (this is a very simple analysis, I'll do some frequency analysis in the future to complete this) ... Let's separate all the color channels:


For the humans:

For dogs:

The first interesting thing is that the Red channel is quite similar to the Green channel for the dogs.

This is the comparison between human channels and dog channels, (red, green, blue respectively)

  

As we can see, the dog curve for the green channel is quite similar to the human curve.


These are the frequency comparison (red, green, blue):

So with this first analysis (a very simple one), I wrote a js script that converts any "human" image into a "dog image".

NOTE: I repeat, this is a first approximation, I need to improve the filter for the red and green channels. You need a brower that supports HTML5 (chrome, Firefox, IE 8). I tested it with PNGs, JPGs and bmps. Other format might not work.

Drop your image FILE here:

Number of people

Another quick and very simple post, A few weeks ago, I was talking with my family about the number of people in a party, how to make everyone know each other and that kind of stuffs. At one moment of the talk my father said: "You cannot know everyone at the party.", then he said: "which is the average of people you may know at the party". Time went by and I kind of forgot the talk, but yesterday a college of mine said (in a complete different talk): "Not everyone knows the same number of people". Then I remember everything and I wondered to myself: "At my father's party, which is the probability of having at least two people that know the same number of people?". By knowing I mean "sometime talked to the guy!"

Think about the problem a bit, there is a trick :-).


Well, the probability is 1. You will always have at least two persons that know the same number of people. The demonstration is really, really simple, the problem is creating a correct model.

Imagine every person at my father's party as a vertex of a Graph (the number of people is n). The act of knowing someone is an edge, and the number of people someone knows is what we call in graph theory: the degree of the vertex.

Let's assume that we cannot find two persons that know the same number of people, in our case, if we order the degree of the vertex for n persons, the only possibility we may have is: {0,1,2,...n-1} (this is call the degree sequence of the graph, and knowing myself is not considered because it's a stupid idea). As we can see on the extremes of the degree sequence (0 and n-1) we have a contradiction, because if the person number 1 doesn't know anyone at the party, then person number n cannot know everyone at the party because it means that he knows number 1 ! (so they know each other)

Damn!, Someone reported a bug, I should get back to work  now! :-)

Have a nice day!

Don't tell anyone

How many times someone told you a secret follow by the phrase: "please, don't tell anyone!"?. This is very common, right?, but what I always say is: "if you want your secrets to be private don't say a word", the most probable thing is that all your friends will know your little secret sooner or later. But is this ok?, I mean, is this the most probable thing?.

Well, graph theory is quite useful to figure this out. Let's say you have a group of friends (a big one), and there exist a probability p of telling the secret, this probability is the same on every person and doesn't depend on if the secret has already been told or not. If we say that each person is a vertex of the graph and the action of telling the secret is an edge (A tells B the secret) then we can model our problem very well. Basically, this is the Erdos-Renyi model, so we can use some of its theory to figure this out.

There is an important theorem of Erdos and Renyi: "if G has a minimum degree of at least 1, then G y connected". This means that non of G's vertex is isolated, in our problem this means that non of your friends will end up not knowing your secret.

So what we need to find now is the probability of having a graph with minimum degree greater than zero. In order to do so, we first find the expression of the degree probability of a vertex for a random graph:

For each vertex (one of your friends) we have n taken by k ways to choose k vertices, the probability of having a vertex is p so, the probability of having k vertices is k times p (they are independent). Bah... is very hard to write this in blogger, sorry, it's a binomial distribution!, so the probability of having k vertices is:

if we have a group of 10 friends, and p=0.10, this expression will have this curve:

So if we want to know the probability of having at least one vertex we do:

Which for n=10 friends, we have the following probabilities:

If we read this graphic, telling a secret is not a very good idea, if the probability of telling the secret is more than 0.4 your secret will surely known by ALL your ten friends.

Let's have a graphic idea of the probability of different number of friends:

As we can see in the graph, for the same probability of telling the secret is less probable to this secret to be shared by all your friends if your group number increases. 

So, after this long exercise, we can say: "if you have a secret DON'T TELL ANYONE" :-)

Serious note: Of course this doesn't solve the problem of telling or not the secret, all your friends are different and the probability of telling the secret is not independent, this is just an excuse to talk about Erdos-Renyi model and binomial distributions.

By the way, Erdos was a great mathematician, some people say that he was addicted to coffee, and that's why he could be awake to write all his works, but please, don't tell anyone!

cheers

Quadratic equation

Last weekend I explained the use of quadratic equation to my nephew (basically how to solve the equation). I think he understood, the concept was quite simple, if you have this:

use:

Basically, that's all you need to know at school (and probably for the rest of your life), but after spending the afternoon doing exercises I realized nobody explained my nephew WHY that formula is the solution to the quadratic equation. And then I realized that the most probable thing is that the most used formula in all high school is not well explained. Well that injustice to this beauty of maths has ended!

(this resolution is really, really, really simple!, and can be found in the Rey Pastor's book (a Spanish guy who knew something about math and wrote some books :-) )

Now we find x:

JUSTICE HAS BEEN DONE!, THE TRUTH MUST BE TOLD!

cheers!

Sean problem

Yesterday a friend of mine (a college also) asked me to resolve a problem he had when he was a child. I'll write down the problem as he told me, I'll try to be as specific as possible.

"When he was a child, Sean used to go to Football practices, unfortunately, he didn't live in a nice neighborhood (it was kind of dangerous). He finished his practices between 10 and 11 pm (yes, really late).  In order to return home, he needed to take a bus, and here is when he had to face his everyday problem: He had two bus stops to choose (in this exercise S1 and S2). The bus arrives to the S1 first, and then to the S2. The sport center was at the same distance from each bus stop. But  S2 was more dangerous than S1 (so he didn't want to wait for a long time). Surprisingly, he knew the time the bus spent to go from the bus station to S1 and from S1 to S2 (an average of time, of course), and at that time of the day (from 10 to 11 pm) only one bus took off the bus station but it was not always the same time. His problem: was which bus stop should he choose?"

Well, that's basically the problem. I'll re paraphrase the question: In the case he doesn't loose the bus, which is the probability if choosing S2?

Why I changed the question?, basically because the S2 was more dangerous and we want him to be safe :-), secondly, if the bus didn't arrive to the S1 yet, is kind of obvious that he would wait less if he went to S1.

I'll write the variables of this problem:

x: is the departure time of the bus (from the bus station). From 0  to 60, minutes (we take 10 pm as our zero)
y: is the time when Sean leaves the building. From 0 to 60, minutes (we take 10 pm as our zero)
tss: is the time that Sean spent to walk from the building to the bus station (it's the same time, no matter if it is S1 or S2)
tb1: is the time that the bus spent to go from the bus station to S1.
tb2: is the time that the bus spent to go from the bus station to S2

S2>S1

Basically, he would choose S2 if the bus is between S1 and S2. So we get the probability of that:

So our functions are (I didn't the case of getting exactly at the same time to S2):

I don't know tss, tb1 and tb2, but let's play with some numbers:

So the probability will be:

So if he knew he wasn't going to miss the bus, S2 has low probabilities of success.

Sean, I'll send you my notebook to you just to review it and play with the times!

Number of paths - acyclic graphs

This is a quick post (I should be working now). Yesterday, I heard a college of mine asking: "how many paths are between these two cities?". The guy next to me looked for an answer in Google (as we always do), and found a very interesting forum that solved his problem.

http://boards.straightdope.com/sdmb/showthread.php?t=396094

I personally read it, and I didn't like what I saw. I mean, if you have a problem like this one, please, read something about graph theory.

If you have an acyclic graph things are much simpler, I'll explain how to do this with an example:

Let's say you have the following graph (It also works with undirected graphs):

The length of the longest (possible) path in an acyclic graph is equal to the number of vertices minus 1 (in this case 3) . The adjacency matrix gives us a lot of information. If you multiple this matrix twice, you get:

This new matrix shows the number of paths of length 2 between two vertices, for example, the number of paths of length 2 between v1 and v3 is 1. So if you want to get the number of possible paths you only need to do:

It's not my intention to say that this is the best solution, but I would like to point out that there are other possibilities than algorithms taken from a forum :-).

Then we can talk about graphs with cycles, but I should get back to work!

Cheers!

Common life and Maths

I'm kind of tired of hearing: "I want to be a lawyer, why would I have to study maths?" or "when I'm going to use this crap?!!, I hate maths!". Well, today I'm going to show you an example of why maths are important for common life!

I often go to work by taxi with four people, usually the treat is: each passenger pays 8 dollars, no matter where he gets out the taxi. But the other day the driver said: "I believe the treat is not fare, I think the best way to pay the trip is: when a person arrives to his place he pays what the taximeter says divided by the number of people on the cab (including me)". Everyone agreed, except me, I was kind of confused, I just kept quite and say nothing, I thought: if everyone agree it must be a good treat. But then I thought: "The price of the entire trip is usually more than 20 dollars but never more than 60 so, Is a good treat for the cab driver?"

Let's say the real cost of the trip is:

Each Lambda is the increment of the trip cost each time a person gets out the taxi. On the other hand, the taxi driver receives:

So the difference is:

If we normalize this function:

Now let's analyse the possible set of values:

If we consider that the taxi driver succeeds if he receives the real cost of the trip or more than it, we have

With this function we can count the number of times the difference is zero or is positive, so we calculate the probability of success:

So the taxi driver has low probability of wining more money....... Only if he knew something about maths!

Ockham Principle

Some time ago, a college of mine sent me this by mail:

The subject was "Can you solve it?"

I don't have to tell you that I couldn't think about anything else until I solved the problem!

Take some time and try to solve it yourself........

The solution is:

(take the first number of the Triangle and multiple by 5 à you get (1), take the second number of the triangle and multiply by 3 you get (2) and take the last number of the triangle and multiple by 4 you get (2) )

Well this was not the solution I found, I found this instead:

(Decompose the number in prime numbers, the box (1) are tens (2) are hundreds and (3) the units of the triangle, the hundreds are the only one that are ordered from lo to high; in order to calculata the tens, multiply all the prime numbers but the first one; in order to calculate the hundred multiply all the primes bu the last one; in order to calculate the units multiply all the prime numbers but the last two)

Which is not the easiest solution (of course!!). Is my solution wrong?, well, no. I have an explanation of the my result. This is just another example of the Ockham Theorem J

Cheers!

If you have another solution, do a comment!

The chess board problem

I'm going to copy the style of one of my best friends blog (http://mchouza.wordpress.com/). Today I bring to you a problem (not as difficult as the ones Mariano presents on his blog :-) ), it's the chess board problem (if it has another name sorry).

Imagine you have a chess board of 100 x 100 squares covered with 10000 black pawns. We play a game in which the only legal move is to change, in a single row or column, all the black pawns to white and all the withe to black. Is it possible in a finite number of moves to leave 1990 white paws on the board?

ok, think a few minutes before you continue :-).

This is the kind of problems that seems very difficult at the beginning but at the end we realize is quite simple.

From the statement we can deduce that the order in which the move are made is immaterial and the order of the selected rows and columns is also not important. So we can say that the selected columns and rows are the first ones. So we will have something like this:

So, the equation we need to solve is:

100 (R + C) -2 RC = 1990

Simple, right?. It’s is quite simple to see in that equation that is impossible to obtain an odd number of white pawns by this process. Further, it is now easy to generalize the problem, if the board is of side 2p and the required number of white pawns is 2n the equation is:

p(R + C) – RC = n

In order to solve this equation we revive certain memories of conics. We can remove the linear term from our equation by a change of the variable R = r + k and C = c + k

p(r + c + 2k) – (r + k)( c + k) = n

if k=p

rc = p.p – n

where

r = R- p and c = C - p

For out example we have p=50 and n=1990/2

So we have,

50 x 50 – 1990/2 = 1505 = 5 x 7 x 43

So our solutions are:

r = 5 x 7 , c= 43 => R =85, C = 93

r = -5x7, c=-43 => R= 15, C =7

Not to complicated right J, Hope you enjoy it!

Math and Computers

Hi everyone, the other day I wrote down some modifications to a NLP model and after expending some time doing some calculations (long story), I found out that I had to solve this limit:

So, I didn’t think too much, I opened Mathcad, wrote the equation and got the following solution:

I was very pleased at that moment because I had the solution, but then I thought, what would had happened if I didn’t have a computer?, what would had happened if I was writing my model in a dessert island after a shipwreck?. And then I got worried, I found out that I depend on computers :-(.

After crying for a few hours, I decided to solve this limit without Mathcad, so I opened Mathematica and wrote the same limit (jajaja, just kidding). I started analysing this function, so I draw it in a paper and got something like this:

As we can see, we find symmetry respect on zero and that’s quite encouraging.

Then I remembered that if we have something like, with , then we have:

Where zj is the root j of Q(k).

So I decided to use this property to solve my problem:

So,

Which is kind of similar to the solution we found at the beginning!.

After that, I remembered that my function was symmetric so,

And so my limit was at one step to be solved! I just only needed to divide by two and all my distresses would pass away!, I happily got my solution:

Now I can sleep at night :-)